Mathman: متباينة الوسط الحسابي- الوسط الهندسي.

هذه المتباينة هي أشهر المتباينات و أول متباينة يتدرب عليها الطالب الأولمبي (بعد متباينة مجموع المربعات)، وتعد واحدة من أهم المتباينات و أكثرها استخداما، و تسمى متباينة الوسط الحسابي - الوسط الهندسي ، وتختصر AM-GM و هذه الحروف أتت من الكلمات (Arithmetic Mean and Geometric Mean) وحيث أن المتوسط الحسابي للعددين a,b هو $\frac{a+b}{2}$ بينما يكون المتوسط الهندسي لهما هو $\sqrt{ab}$ . الصورة الأبسط للمتباينة تكون :

متباينة AM-GM الأساسية: إذا كان a,b أعدادا حقيقية موجبة فإن:

$\frac{a+b}{2}\ge\sqrt{ab}$

وتتحقق المساواة إذا و فقط إذا كان a=b.

البرهان: المتباينة تكافئ تماما:

$\left(\sqrt a-\sqrt b\right)^2\ge0$

وهي صحيحة لأن أي مربع أكبر من الصفر. ومن الواضح أن المساواة تتحقق عندما a=b فقط.

لهذه المتباينة الأثر الكبير في المتباينات الأخرى (حتى تعميمها)، نتعرض لهذا المثال الشهير، وهو أيضا مفيد لحل متباينات أولمبية أخرى.

مثال 1: إذا كان a,b,c أعداد حقيقية موجبة، فبرهن أن:

$a^2+b^2+c^2\ge ab+bc+ac$

البرهان:

$\left.\begin{matrix} a^2+b^2\ge 2ab\\ b^2+c^2\ge 2bc\\ c^2+a^2\ge 2ca \end{matrix}\right\} \Rightarrow 2(a^2+b^2+c^2)\ge 2(ab+bc+ac)$

وبالقسمة على 2 ينتج المطلوب مباشرة.

برهان آخر: في الحقيقة هو يمكن استنتاجه من البرهان الأول (لماذا؟)

$\begin{align*}a^2+b^2+c^2&\ge ab+bc+ac\\\Leftrightarrow 2a^2+2b^2+2c^2&\ge 2ab+2bc+2ac\\\Leftrightarrow(a-b)^2+(b-c)^2+(c-a)^2&\ge 0\end{align*}$

والعبارة الأخيرة صحيحة لأنها عبارة عن مجموع مربعات.

الآن نأتي للتعميم، تعميم نظرية AM-GM سهل و بسيط، و بدل أن يكون لدينا متغيرين، سيكون لدينا n من المتغيرات.

متباينة AM-GM المعممة: إذا كان 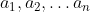$a_1,a_2,\ldots a_n$ أعداد حقيقية موجبة، فإن

$\frac{a_1+a_2+\cdots +a_n}{n}\ge\sqrt[n]{a_1a_2\cdots a_n}$

والمساواة تتحقق عندما $a_1=a_2=\ldots=a_n$ .

البرهان: لطوله، سأضع فقط هذا الرابط لموسوعة ويكيبيديا.

مثال 2: إذا كان a,b,c أعداد حقيقية غير سالبة، فبرهن أن
$(a+b)(b+c)(c+a)\ge 8abc$ البرهان: ببساطة
$(a+b)(b+c)(c+a)\ge \left(2\sqrt{ab}\right)\left(2\sqrt{bc}\right)\left(2\sqrt{ac}\right)=8abc$ وهو المطلوب.

أحيانا تحتاج المسألة لأكثر من الحل المباشر.

مثال 3: إذا كان a,b,c أعداد حقيقية موجبة، فبرهن أن
$\frac{a^3}{bc}+\frac{b^3}{ca}+\frac{c^3}{ab}\ge a+b+c$
البرهان: واضح أن الحل المباشر لا يأتي بنتيجة أبدا، لأنه يعطي حدا واحدا، بينما في الطرف الأيمن يوجد 3 حدود، لذا سنستخدم المتباينة 3 مرات لإنتاج كل حد على الطرف الأيمن.
$\left. \begin{align*}\frac{a^3}{bc}+b+c&\ge 3a\\\frac{b^3}{ca}+c+a&\ge 3b\\\frac{c^3}{ab}+a+b&\ge 3c\end{align*}\right\}\\\Rightarrow \frac{a^3}{bc}+\frac{b^3}{ac}+\frac{c^3}{ab}+2(a+b+c)\ge 3(a+b+c)$ وينتج المطلوب مباشرة.

خذ المسائل التالية على شكل تمارين.