متباينة الأوساط الأربعة: إذا كان 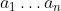 أعداد حقيقية موجبة فإن:
أعداد حقيقية موجبة فإن:
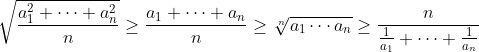 وتتحقق المساواة عندما تتساوى المتغيرات كلها.
وتتحقق المساواة عندما تتساوى المتغيرات كلها.
مع أن السابقة حالة خاصة أيضا، إلا أنها أسهل استخداما، وكذلك فهي مهمة. المتباينة التالية هي أيضا تعميم للسابقة (يبدو أنك مللت التعاميم :) ) متباينة الأوساط: إذا كان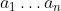 أعداد حقيقية موجبة و كان:
أعداد حقيقية موجبة و كان: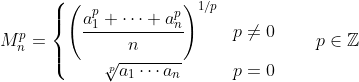 فإن
فإن 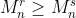 لكل
لكل 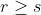 حيث r,s أعداد صحيحة.
حيث r,s أعداد صحيحة.
لا أنكر أن المتباينة السابقة ذات استخدام نادر. حاليا، لا يحضرني متباينة تستخدم أي من الإثنتين، لكنك إن دخلت هذا العلم ستجد تطبيقاتها منتشرة جدا. يمكن تعيمها مرة أخرى لتصبح
متباينة الأوساط المعممة: بنفس الشروط نجد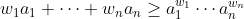 حيث
حيث 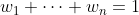 . أحد تطبيقات هذه المسألة تجدها هنا.
. أحد تطبيقات هذه المسألة تجدها هنا.
تلك متباينات على طالب الأولمبياد أن يعيها، لكن المشكلة ليست في عدد النظريات و الحقائق التي تعرفها، العبرة في كيفية استخدامها و التحكم بها لصالحك، هذه أهم نقطة في استخدام تلك المتباينات.
جمعت لك من خلال خبرتي البسيطة بعض طرق استخدامها و توظيفها لتحقيق المطلوب.
1- إستخدم عملية الجمع! أقصد إن وجدت مثل هذه المسألة (abc=1)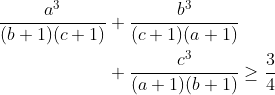 لاحظ إنه لو استخدمت المتباينة بشكل مباشر، فإنك لن تصل إلا نتيجة، بالتالي نحاول التخلص من المقامات بحركة الجمع، وهي
لاحظ إنه لو استخدمت المتباينة بشكل مباشر، فإنك لن تصل إلا نتيجة، بالتالي نحاول التخلص من المقامات بحركة الجمع، وهي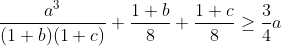 بنفس الطريقة نجد أننا نقترب من الحل، حيث أننا نقوم بعمل نفس الطريقة للحدود الثلاثة، ثم نجمعها و نحصل على متباينة جديدة توصل إلى الحل. أيضا هذه المتباينة التي سبق شرحها
بنفس الطريقة نجد أننا نقترب من الحل، حيث أننا نقوم بعمل نفس الطريقة للحدود الثلاثة، ثم نجمعها و نحصل على متباينة جديدة توصل إلى الحل. أيضا هذه المتباينة التي سبق شرحها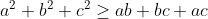 (جربها بنفسك).
(جربها بنفسك).
2- الإختيار الجيد للمتغيرات. إختيار المتغيرات بشكل جيد هي الأكثر أهمية، وهذه تكتسب بالخبرة، ولا تنس: إن كان لديك كسر فإنه يقل (قيمة) كلما كبر المقام، بمعنى أنك تستطيع تكبر الكسر بتصغير المقام و العكس صحيح، حيث أن الكثير يخطأ في هذه الملاحظة في البداية.
3- طريقة كوشي شواز: طريقة عكسية مفيدة جدا، فمثلا (a+b+c=3)
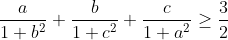 نعمل على التالي:
نعمل على التالي:
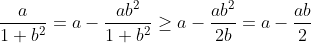 و عمل هذا لجميع الحدود يقربك من الحل. فكرة هذه الطريقة أنك إن لم تكن تستطيع استخدام متباينة الوسط الحسابي-الوسط الهندسي فعليك تحويل الكسر إلى سالب ثم استعمالها للمقام (إذا كان الكسر كلما قل المقام قل قيمة).
و عمل هذا لجميع الحدود يقربك من الحل. فكرة هذه الطريقة أنك إن لم تكن تستطيع استخدام متباينة الوسط الحسابي-الوسط الهندسي فعليك تحويل الكسر إلى سالب ثم استعمالها للمقام (إذا كان الكسر كلما قل المقام قل قيمة).
4- معرفة المساواة! معرفة المساواة هي مهمة جدا! فمثلا في المسألة السابقة (abc=1):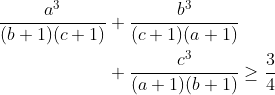 واضح أن المساواة تحدث عند a=b=c=1، وهذا ما جعلنا نبتعد عن استخدام
واضح أن المساواة تحدث عند a=b=c=1، وهذا ما جعلنا نبتعد عن استخدام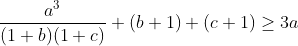 لأن المساواة لن تتحقق أبدا فنكون نبحث في دائرة مغلقة. بالتالي البعض يحل أنظمة من المعادلات للتأكد من صحة الخطوة، لذا عليك التحقق متى ستحدث المساواة عند كل خطوة.
لأن المساواة لن تتحقق أبدا فنكون نبحث في دائرة مغلقة. بالتالي البعض يحل أنظمة من المعادلات للتأكد من صحة الخطوة، لذا عليك التحقق متى ستحدث المساواة عند كل خطوة.
5- يجب أن يكون لديك خلفية لا بأس بها في العمليات الجبرية و المتطابقات، معرفتها يسهل عليك تحويل المتباينة إلى صورة أخرى، وأحيانا الإستفادة من الشرط المعطى (إن كان لديك شرط في السؤال)، وستستزيد منها حسب خبرتك في المتباينات و المعادلات و نظرية العدد و العمليات الجبرية!
6- الاستمرار في الحل.
سأتكلم عن كل نقطة عندما تسنح الفرصة في مشاركة جديدة بإذن الله، حاول أن تحل ما سبق.
مع أن السابقة حالة خاصة أيضا، إلا أنها أسهل استخداما، وكذلك فهي مهمة. المتباينة التالية هي أيضا تعميم للسابقة (يبدو أنك مللت التعاميم :) ) متباينة الأوساط: إذا كان
لا أنكر أن المتباينة السابقة ذات استخدام نادر. حاليا، لا يحضرني متباينة تستخدم أي من الإثنتين، لكنك إن دخلت هذا العلم ستجد تطبيقاتها منتشرة جدا. يمكن تعيمها مرة أخرى لتصبح
متباينة الأوساط المعممة: بنفس الشروط نجد
تلك متباينات على طالب الأولمبياد أن يعيها، لكن المشكلة ليست في عدد النظريات و الحقائق التي تعرفها، العبرة في كيفية استخدامها و التحكم بها لصالحك، هذه أهم نقطة في استخدام تلك المتباينات.
جمعت لك من خلال خبرتي البسيطة بعض طرق استخدامها و توظيفها لتحقيق المطلوب.
1- إستخدم عملية الجمع! أقصد إن وجدت مثل هذه المسألة (abc=1)
2- الإختيار الجيد للمتغيرات. إختيار المتغيرات بشكل جيد هي الأكثر أهمية، وهذه تكتسب بالخبرة، ولا تنس: إن كان لديك كسر فإنه يقل (قيمة) كلما كبر المقام، بمعنى أنك تستطيع تكبر الكسر بتصغير المقام و العكس صحيح، حيث أن الكثير يخطأ في هذه الملاحظة في البداية.
3- طريقة كوشي شواز: طريقة عكسية مفيدة جدا، فمثلا (a+b+c=3)
4- معرفة المساواة! معرفة المساواة هي مهمة جدا! فمثلا في المسألة السابقة (abc=1):
5- يجب أن يكون لديك خلفية لا بأس بها في العمليات الجبرية و المتطابقات، معرفتها يسهل عليك تحويل المتباينة إلى صورة أخرى، وأحيانا الإستفادة من الشرط المعطى (إن كان لديك شرط في السؤال)، وستستزيد منها حسب خبرتك في المتباينات و المعادلات و نظرية العدد و العمليات الجبرية!
6- الاستمرار في الحل.
سأتكلم عن كل نقطة عندما تسنح الفرصة في مشاركة جديدة بإذن الله، حاول أن تحل ما سبق.